фигурное катание...
-
вопрос, как преобразовать показатели комад из 2х табоиц в одну общую.
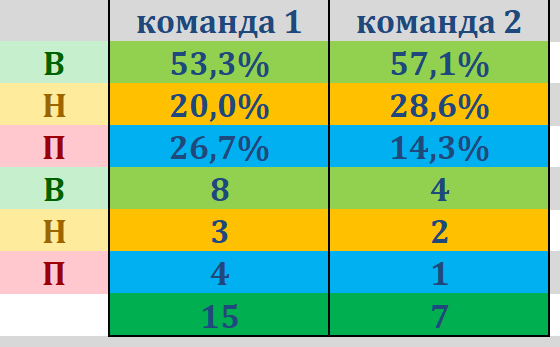
и можем ли мы так делать?
-
это что значит - "преобразовать показатели"?)
-
выставить линию для 1х2 исходя из общих данных..
-
-
ком1 ком2 п1 х п2в 50,00% 85,00% 27,50% 20,00% 52,50%
н 30,00% 10,00%
п 20,00% 5,00%
в 5 17
н 3 2
п 2 1
10 20не уверен что п2 85% должна в реале понизится до 52%..
но все же к большинству то матчей можно применять данную формулу! -
если на пальцах: встречается команда 1 которая проигрывает только два матча из 10 с ком 2 которая выигрывает >8 из 10 => по сути равные команды, кэф 2.0, победа ком2 будет 52,5% , х2 72,5% соответственно.
фишка в том, что все игры с разными соперниками, качество соперников не известно и в данном случае их разное количество, поэтому вилами по воде. у меня был трояк по математике - возможно меня поправят)
-
ну суть понятна в каком направлении идти, твой вариант вполне подходит для общей оценки большинство матчей.
-
для общей оценки большинства матчей есть линия бк)
Пользователь @iforpagem написал в фигурное катание...:
ком1 ком2 п1 х п2в 50,00% 85,00% 27,50% 20,00% 52,50%
н 30,00% 10,00%
п 20,00% 5,00%
в 5 17
н 3 2
п 2 1
10 20не уверен что п2 85% должна в реале понизится до 52%..
но все же к большинству то матчей можно применять данную формулу!p.s. этим способом вряд ли получится находить валуи
-
задача выставить правильный кф..
ком1 ком2 п1 х п2
50,00% 85,00% 27,50% 30,00% 42,50%
50,00% 10,00%
0,00% 5,00%
5 17
5 2
0 1
10 20вот пример, п2 явно тут будет занижен.
-
@iforpagem ну так правильно, ком1 согласно внп вообще не проигрывает)
-
у первой команды 5 побед и 5 ничьих
-
"задача выставить правильный кф.." - это и есть кнопка бабло
-
у второй статус полуфиналиста лч... 17/2/1
-
нет, это сейчас простая математика.. она к спорту вообще не относится.
-
@iforpagem и ноль поражений
-
ну понятно, логика то говорит о том что вторая победит скорее всего.
-
Пользователь @iforpagem написал в фигурное катание...:
выставить линию для 1х2 исходя из общих данных..
и можем ли мы так делать?Можем. Но смысла в этом мало.
Приведу аналогию. Допустим, нам известны два шахматиста: А и Б.
А выиграл 5 игр из 10 неизвестно у кого. Б выиграл 4 игры из 7 неизвестно у кого. Ничьих, для упрощения, не было.
Как они сыграют между собой? Т.е., например, какова ожидаемая разница их elo-рейтинга?
Можно даже ТОЧНО подсчитать, предположив равенство рейтингов их соперников - дурное дело не хитрое. :) Допустим, получится 157 (взято с потолка). Но какая будет наша уверенность в этой оценке? Почти никакая: плюс-минус 2000, наверно. :)Так что, стоит ли выставлять линию на шахматистов с разницей рейтинга 157±2000? Думаю, валуйностью тут явно не пахнет.
-
вообще да, при таких условиях только за счет отсебятины можно выставить приемлемый кф.
насчет эло тоже думал что можно использовать для анализа и насколько он хорош, только непонятно как его спроектировать, даже представления нету.насчет моего выше упомянутого вопроса, такую вот мини формулу сцепил:
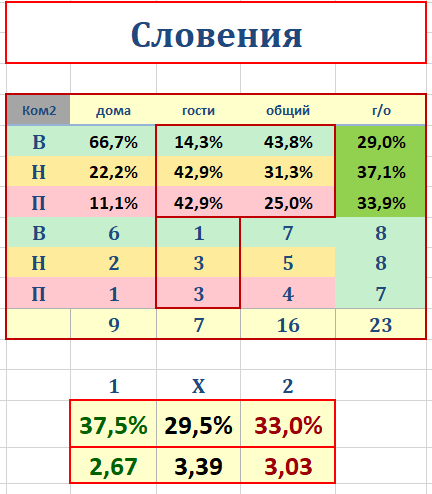
с виду вроде норм по цифрам получается.. да и время должно ускорить на просмотры событий..
-
Пользователь @iforpagem написал в фигурное катание...:
вообще да, при таких условиях только за счет отсебятины можно выставить приемлемый кф.
Не, в том-то и дело, что приемлемый не выйдет никак. Просто знаний не будет хватать.
Вы играете против тех, кто владеет информацией лучше вас (больше знает, глубже изучал конкретные игры этих конкретных команд). Такое очень мало похоже на плюсовую игру.В плюс можно было бы рассчитывать играть, если бы и другие ставочники/буки тоже ничего не знали об этих командах, и для них тоже уверенность в их оценке была бы ±2000 (желательно, ±3000 :).
Когда же вы играете со своими 157±2000 против чужих -63±150, вы можете даже думать что более правильно оцениваете кто является фаворитом. Но ни к чему хорошему это обычно не приводит, потому как не должно.
насчет эло тоже думал что можно использовать для анализа и насколько он хорош, только непонятно как его спроектировать, даже представления нету.
Старый добрый elo основан на вполне примитивном соотношении (кажется, это из работ 1920х годов - точно не помню). Когда каждому сопернику присваивается некая "сила" (возьмём, например, A для первого, B для второго) и тогда вероятность победы первого над вторым оценивается как A/(A+B).
Переход из этой "силы" в elo - это просто перенормировка: A = 10^(Ra/400), откуда elo-рейтинг Ra = 400*lg(A).
Отсюда вытекает известная формула вероятности победы (или матожидания количества очков за одну игру в случае шахмат):
A/(A+B) = 10^(Ra/400) / (10^(Ra/400) + 10^(Rb/400)) = 1 / (1 + 10^((Rb-Ra)/400))Так что в расчётах зачастую удобнее пользоваться не рейтингами Ra и Rb, а непосредственно силами A и B. Однако, это вполне примитивная система.
Основной, а может и главный, недостаток: если А сильнее Б, Б сильнее В, то, согласно этой схеме, А должен быть сильнее В. На практике же часто можно наблюдать что А может быть слабее В.