Как решит эту задачу .?

Новичок

Вероятности угадать в ТОТО 15
09 из 15 = 2^6101112131415/(3^15123456) = 1:45

Новичок

Вероятности угадать в ТОТО 15
09 из 15 = 2^6101112131415/(3^15123456) = 1:45

DimOK

Так нельзя считать, вы предполагаете, что все исходы равновероятны, а это совсем не так.

DmitriyD

@новичок если все исходы равновероятны то вот так посчитать можно если нет то нужно найти среднюю вероятность сложись все выборы кубона и разделить на кол событий и вставить вместо 1/3 в формуле могу ошибаться я не математик но сам делаю так и вроде все сходится), я таким образом пытался найти бриф без пересечений типо идеальный если кф получается без остатка типо как в 15 категории то значит есть шанс что есть пакет без пересечений 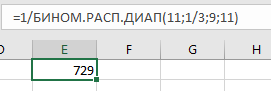вот например вероятность из 11 угадать 9и выше 1из729, 729 без остатка целое число и как раз ту есть бриф из 729 купонов- это бриф 13 категории 11 тройников, бриф я всетаки нашел идеальный которого нет в лягухе)

Новичок

Лягуха дает теже самые 729 вариантов по 13 кате . Или ваш именно на 15 игр

DmitriyD

@новичок я это привел в пример просто заранее зная что пакет уже есть, если по расчетам получается без остатка ровно 729 то и скорей всего есть пакет такой . Таким же способом можно попытаться другие пакеты найти которых нет в лягухе

desm

Пользователь @новичок написал в Как решит эту задачу .?:

Насчёт ТОТО я не очень в курсе.
Но когда речь о событиях разной вероятности, я пользуюсь своей прогой на Питоне.
Например, для подсчёта вероятностей встретить определённое количество скаттеров в каком-то слоте (барабаны часто разной длины и имеют разное количество скаттеров).

import pprint, collections

def binom_ext(p):
    '''p - массив вероятностей успеха в каждом испытании
    Возвращает для каждого числа успехов кортеж (вероятность, 1/вероятность)'''
    n = len(p)
    out = collections.defaultdict(int)
    for i in range(2**n):
        i = '{0:0{1}b}'.format(i, n)
        x = sum([ c=='1'  for c in i ])
        pp = 1
        for c,p_ in zip(i,p):  pp *= p_  if c=='1' else  1-p_
        if pp:  out[x] += pp
##        print(i, x, pp)
    print(sum(out.values()))
    out = { k:(v,1/v)  for k,v in out.items() }
    pprint.pprint(out)
    return out


binom_ext([3/29, 6/41, 3/42, 3/41, 3/42])   # Hall of Gods slot, scatters
binom_ext([0, 0, 9/42, 9/41, 9/42])         # Hall of Gods slot, bonus