Формула вычисления форы.
-
Дано:
1X2
O/U
BTS
Нужно найти фору.
Вот приблизительную вероятность на двойной шанс, например 1X, найти просто, надо сложить вероятности П1 и ничьей.
А как найти вероятность, например, Ф1(+1) или Ф1(-1.5)? -
Футбол?
Достаточно 1х2 и O/U для вычисления всего.
Нужно построить матрицу счетов, откуда достаются все остальные вероятности. -
-
так считаю в экселе.. фора1 +1
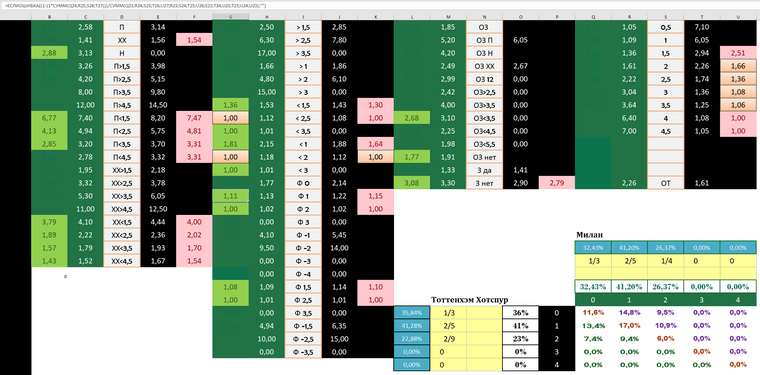
-
Универсальной формулы нет? Без построения матриц?
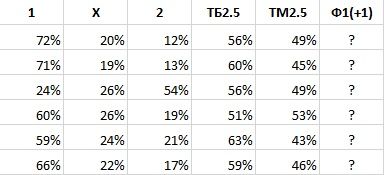
-
Целочисленная фора всегда рассчитывается из ближайших половинчатых
-
Пользователь @Iforpagem написал в Формула вычисления форы.:
так считаю в экселе.. фора1 +1
По вашей формуле получается: (1-Х)/(П1+X), но не учитываются тоталы...
-
Пользователь @TverReus написал в Формула вычисления форы.:
Целочисленная фора всегда рассчитывается из ближайших половинчатых
-Не подскажите который час?
-Ну для этого мне нужно посмотреть на часы... -
@Vasya нет, нужно вычесть возврат и поделить на остаток победы.
вот фора -3 =ЕСЛИОШИБКА((1-(1*СУММ(T23;U24)))/СУММ(U23);"")
тут тотал не учитывается так как напрямую суммируются все нужные счета.
может можно и по другому считать хз я методом тыка перебирал и подобрал, попробуй тоже тыкать пару дней может получиться свою фору оптимальную подобрать. -
Все ниже только про вероятности
ф1(-1,5) п1(=1) ф2(+0,5) - полный набор исходов. П1 в 2 гола и больше, П1 ровно в 1 гол, Х2Дальше нужно "нормировать" вероятности крайних исходов для получения целочисленных значений форы
Нормировать - посчитать относительную величину каждого исхода относительно величины ( 1 - П1(=1) )
И нужно заметить, что ( 1 - П1(=1) ) = ф1(-1,5) + ф2(+0,5)ф1(-1) = ф1(-1,5) / ф1(-1,5) + ф2(+0,5)
ф2(+1) = ф2(+0,5) / ф1(-1,5) + ф2(+0,5) -
Всё понял, то есть без процентов на каждый исход Ф(+1) не посчитать, ибо у меня в архиве только 1X2, тотал и BTTS...
-
У вас в архиве данные только для форы -0.5 (победа), чтобы посчитать -1 нужно знать ещё -1.5, которых у вас нет.
-
Пользователь @DimOK написал в Формула вычисления форы.:
У вас в архиве данные только для форы -0.5 (победа), чтобы посчитать -1 нужно знать ещё -1.5, которых у вас нет.
Это всё пострасчёты - найти нужную фору с помощью двух других. Но вопрос был не об этом.
Вопрос был - можно ли вычислить по какой-либо хитрой формуле вероятность определённой форы с помощью того, что дано в первом посте, хотя бы приблизительно совпадающую с той, что дают буки.
Ведь данных довольно достаточно, интерполировать как-то это всё... -
Это всё будут приближения и допущения, как та же самая матрица, которую можно построить, допуская что распределение голов нормальное, она будет не очень точной. но похожей на правду.
-
@Vasya -можно ли вычислить по какой-либо хитрой формуле вероятность определённой форы с помощью того, что дано в первом посте, хотя бы приблизительно совпадающую с той, что дают буки.
ты хочешь одной формулой подобрать кф букмейкера, у них у самих кф отличаются друг от друга.
если тебе нужен твой личный кф на фору для сравнения с букмейкером
то можно исходя из базы отобрать события похожие друг на друга, к примеру п1 (1.40-1.60) х (3.20-4.4) при тб2.5 +-50%, или от андердога посмотреть нужные кефы из отобранных матчей вывести нужную фору в проценты, условно п1 оказалось 30% возврат 50% п2 20%(это результат подсчета нужной форы) затем из этого посчитать какой должна быть фора. если не ошибаюсь 1-50%/20% =2.5 -
Для нахождения вероятности практически любого исхода у вас есть все данные - 1х2+тотал.
Знаете, что такое математическое ожидание?
Из базы и коэффициентов тотала сможете достать МО голов в матче?И да, задачка всем неравнодушным на подумать.
Есть тотал 2.5 с кефами 1.9-1.9, т.е. с вероятностями 0,5-0,5.
Сколько голов (в среднем) будет забито в 1000 таких матчей, если считать, что оценка тотала максимально правильная? -
Всем спасибо за ответы, проблема решена, нашёл айдишки к архиву. Осталось только запарсить...
-
Пользователь @TverReus написал в Формула вычисления форы.:
Сколько голов (в среднем) будет забито в 1000 таких матчей, если считать, что оценка тотала максимально правильная?
Это было бы замечательно, если бы работало.
Тоталы команд не являются независимыми событиями, увы.
Решение задачи "в лоб" сильно занизит вероятность ничьих.